数据结构与算法学习之链表
2019-10-16 21:27:24 #数据结构与算法

链表

动态数组有个明显的缺点，可能会造成内存空间的大量浪费；能否用到多少就申请多少内存？链表可以办到这一点。

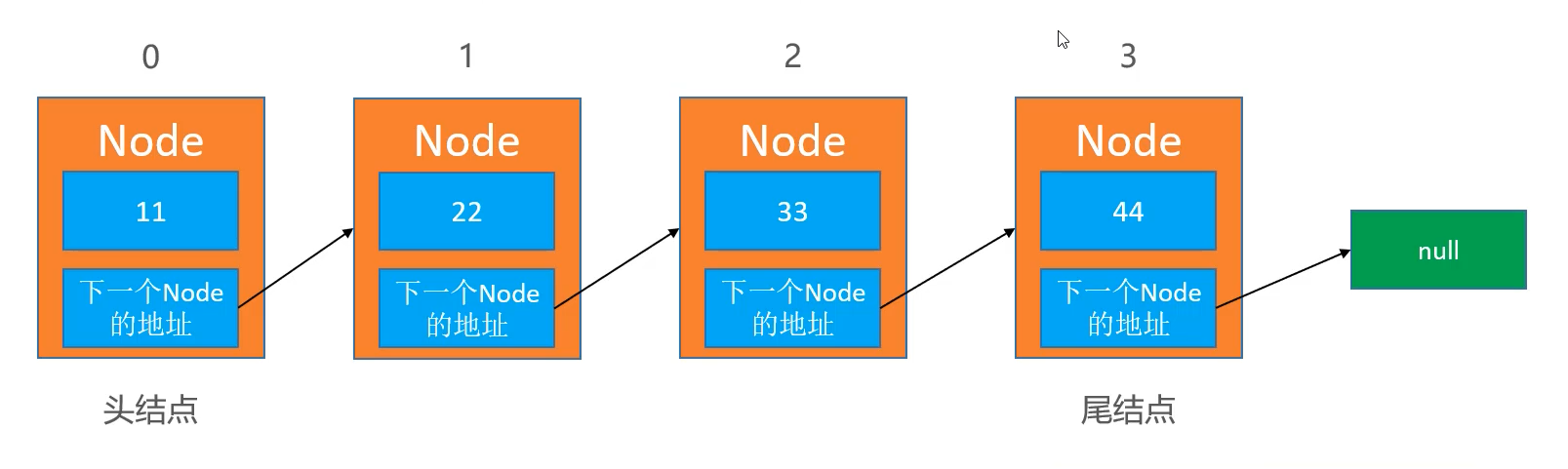
链表是一种链式存储的线性表，所有元素的内存地址不一定是连续的：

链表的设计

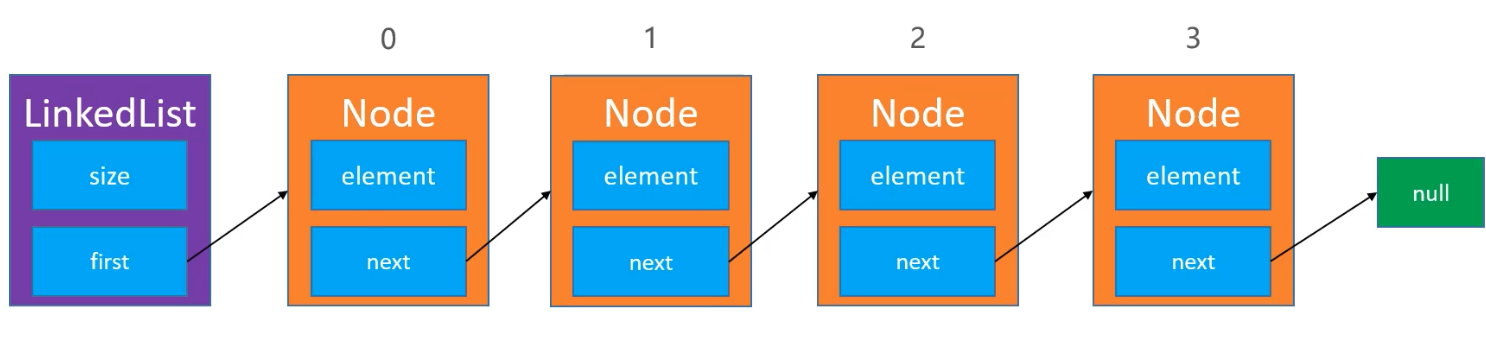
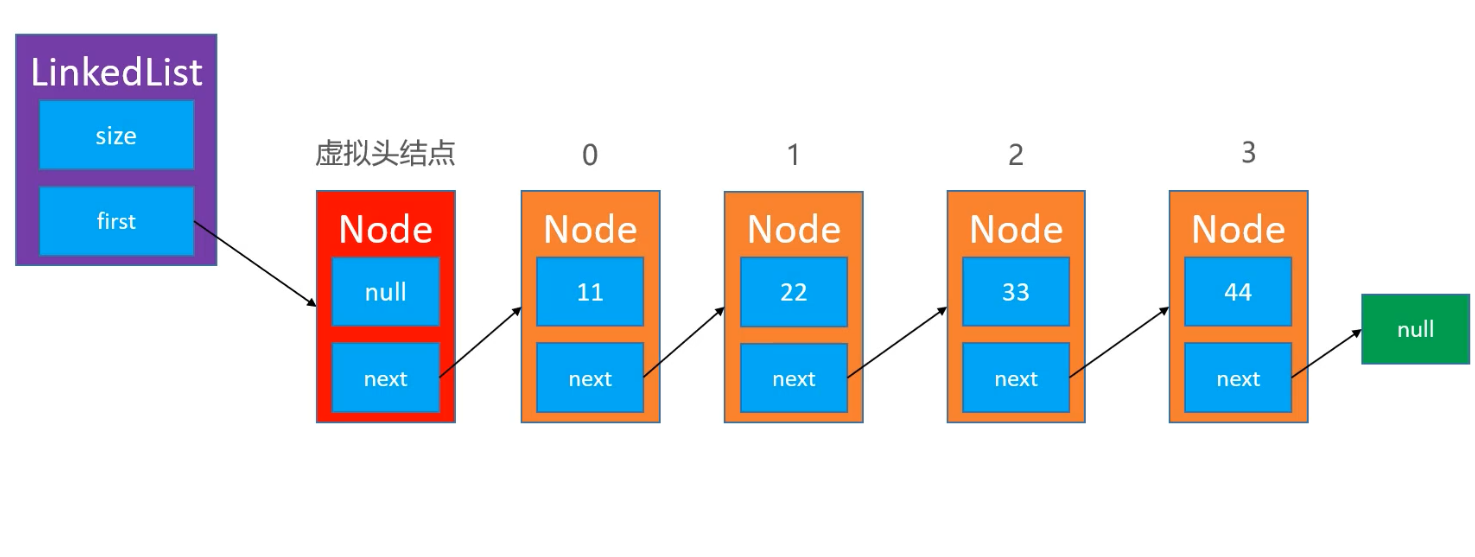
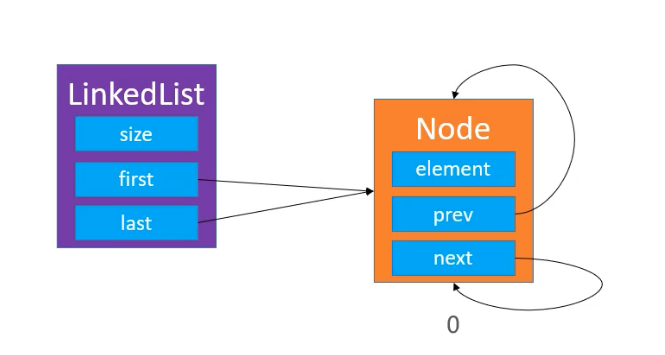
在 LinkedList 类中，有成员变量 size 和指向头节点的 first ，内部类 Node 中存储了变量值 element，和指向下一个节点的 next。

接口设计

链表的大部分接口和动态数组是一致的，所以我们可以用 java 的一个语法——接口来实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
package com.mahoo;

public interface List<E> {
	static final int ELEMENT_NOT_FOUND = -1;
	/**
	 * 清除所有元素
	 */
	void clear();

	/**
	 * 元素的数量
	 * @return
	 */
	int size();

	/**
	 * 是否为空
	 * @return
	 */
	boolean isEmpty();

	/**
	 * 是否包含某个元素
	 * @param element
	 * @return
	 */
	boolean contains(E element);

	/**
	 * 添加元素到尾部
	 * @param element
	 */
	void add(E element);

	/**
	 * 获取index位置的元素
	 * @param index
	 * @return
	 */
	E get(int index);

	/**
	 * 设置index位置的元素
	 * @param index
	 * @param element
	 * @return 原来的元素ֵ
	 */
	E set(int index, E element);

	/**
	 * 在index位置插入一个元素
	 * @param index
	 * @param element
	 */
	void add(int index, E element);

	/**
	 * 删除index位置的元素
	 * @param index
	 * @return
	 */
	E remove(int index);

	/**
	 * 查看元素的索引
	 * @param element
	 * @return
	 */
	int indexOf(E element);
}

当具体编码时可以发现，还有一些代码是可以共用的，没必要重写接口的方法，也就是可以抽离出来通用的，例如int size();方法直接返回 size 即可。

接口内部，并不能对方法具体实现，它只是声明外界需要实现哪些方法，这时候需要怎么做呢？

我们可以再创建一个类，作为动态数组和链表的父类，并且声明为抽象类，也就是，只能被继承，不能有实例化，而且不需要具体实现接口的方法。

然后用这个抽象父类去实现接口的方法，并将公共的代码放在其中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
package com.mahoo;

public abstract class AbstractList<E> implements List<E>  {
	/**
	 * 元素的数量
	 */
	protected int size;
	/**
	 * 元素的数量
	 * @return
	 */
	public int size() {
		return size;
	}

	/**
	 * 是否为空
	 * @return
	 */
	public boolean isEmpty() {
		 return size == 0;
	}

	/**
	 * 是否包含某个元素
	 * @param element
	 * @return
	 */
	public boolean contains(E element) {
		return indexOf(element) != ELEMENT_NOT_FOUND;
	}

	/**
	 * 添加元素到尾部
	 * @param element
	 */
	public void add(E element) {
		add(size, element);
	}
	
	protected void outOfBounds(int index) {
		throw new IndexOutOfBoundsException("Index:" + index + ", Size:" + size);
	}
	
	protected void rangeCheck(int index) {
		if (index < 0 || index >= size) {
			outOfBounds(index);
		}
	}
	
	protected void rangeCheckForAdd(int index) {
		if (index < 0 || index > size) {
			outOfBounds(index);
		}
	}
}

注意，这里将ELEMENT_NOT_FOUND 公共常量的声明放在了 List 接口中，其实也是可以放在抽象的父类 AbstractList中的，这样子类也同样可以访问到；但从设计的角度考量，这样的作法是欠妥帖的，因为AbstractList在使用其子类的时候是不可见的，它只是抽离公共代码的一个中间层，所以可见的公共常量就不应放在这里。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
package com.mahoo;

public abstract class AbstractList<E> implements List<E> {
	/**
	 * 元素的数量
	 */
	protected int size;

	/**
	 * 元素的数量
	 * 
	 * @return
	 */
	public int size() {
		return size;
	}

	/**
	 * 是否为空
	 * 
	 * @return
	 */
	public boolean isEmpty() {
		return size == 0;
	}

	/**
	 * 是否包含某个元素
	 * 
	 * @param element
	 * @return
	 */
	public boolean contains(E element) {
		return indexOf(element) != ELEMENT_NOT_FOUND;
	}

	/**
	 * 添加元素到尾部
	 * 
	 * @param element
	 */
	public void add(E element) {
		add(size, element);
	}

	protected void outOfBounds(int index) {
		throw new IndexOutOfBoundsException("Index:" + index + ", Size:" + size);
	}

	protected void rangeCheck(int index) {
		if (index < 0 || index >= size) {
			outOfBounds(index);
		}
	}

	protected void rangeCheckForAdd(int index) {
		if (index < 0 || index > size) {
			outOfBounds(index);
		}
	}
}

经过上述操作，我们的链表只需要继承抽象父类 AbstractList，并创建一个 Node 内部类即可，IDE 会提醒其他的接口实现，我们一个一个慢慢来：

1
2
3
4
5
6
7
8
9
10
11
12
13
public class LinkedList<E> extends AbstractList<E> {
    private Node<E> firstNode;

    private static class Node<E> {
        E element;
        Node<E> next;

        public Node(E element, Node<E> next) {
            this.element = element;
            this.next = next;
        }
    }
}

清空元素

清空链表，只需要将头节点置为空，切断与其它节点的连接即可，剩下的交给 GC ，记得还要将 size 值赋为 0：

1
2
3
4
5
@Override
public void clear() {
    firstNode = null;
    size = 0;
}

添加元素

当某个在位置添加元素时，我们首先要确定这个位置前一个位置的节点，才能根据链表的特性去寻找后面的节点，为了方便，我们可以将寻找节点封装成一个内部方法：

1
2
3
4
5
6
7
8
9
10
private Node<E> node(int index) {
    rangeCheck(index);
    // 拿到头节点
    Node<E> node = firstNode;
    for (int i = 0; i < index; i++) {
        // 通过 next 拿到下一个节点
        node = node.next;
    }
    return node;
}

其实这样一来，set 和 get 方法就很好实现了：

1
2
3
4
5
6
7
8
9
10
public E get(int index) {
    return node(index).element;
}

public E set(int index, E element) {
    Node<E> node = node(index);
    E old = node.element;
    node.element = element;
    return old;
}

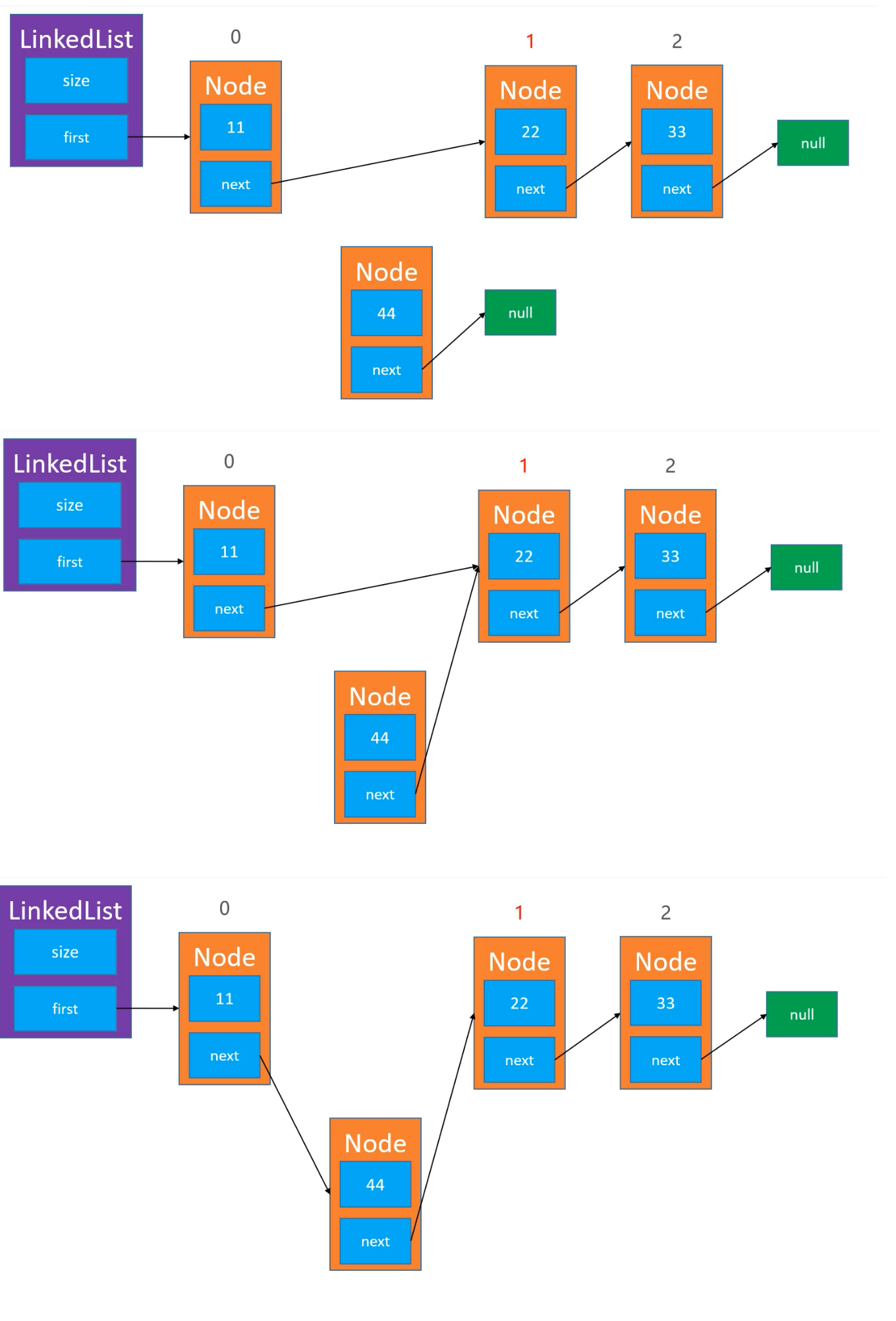
继续回到正题，当添加元素时，拿到前一个节点后，首先将传入的值和此节点的 next 节点作为初值创建一个新节点，之后再将此节点的 next 指向新创建的待添加节点；不过还要考虑一种特殊情况，也就是 index = 0 的情况，这会在rangeCheck()报错，所以 index = 0 需要特殊处理；index = 0 时也就是往头结点位置添加节点，其实很简单，将 firstNode（图中为 first ） 作为参数创建新节点，再让 firstNode 指向新创建的节点即可，最后不要忘记 size++：

1
2
3
4
5
6
7
8
9
10
public void add(int index, E element) {
    if (index == 0) {
        firstNode = new Node<E>(element, firstNode);
    } else {
        Node<E> prevNode = node(index - 1);
        Node<E> node = new Node<E>(element, prevNode.next);
        prevNode.next = node;
    }
    size++;
}

处理了 index = 0 这个特殊情况，index = size 这种情况上述代码也是完全能够处理的，就不多言了。

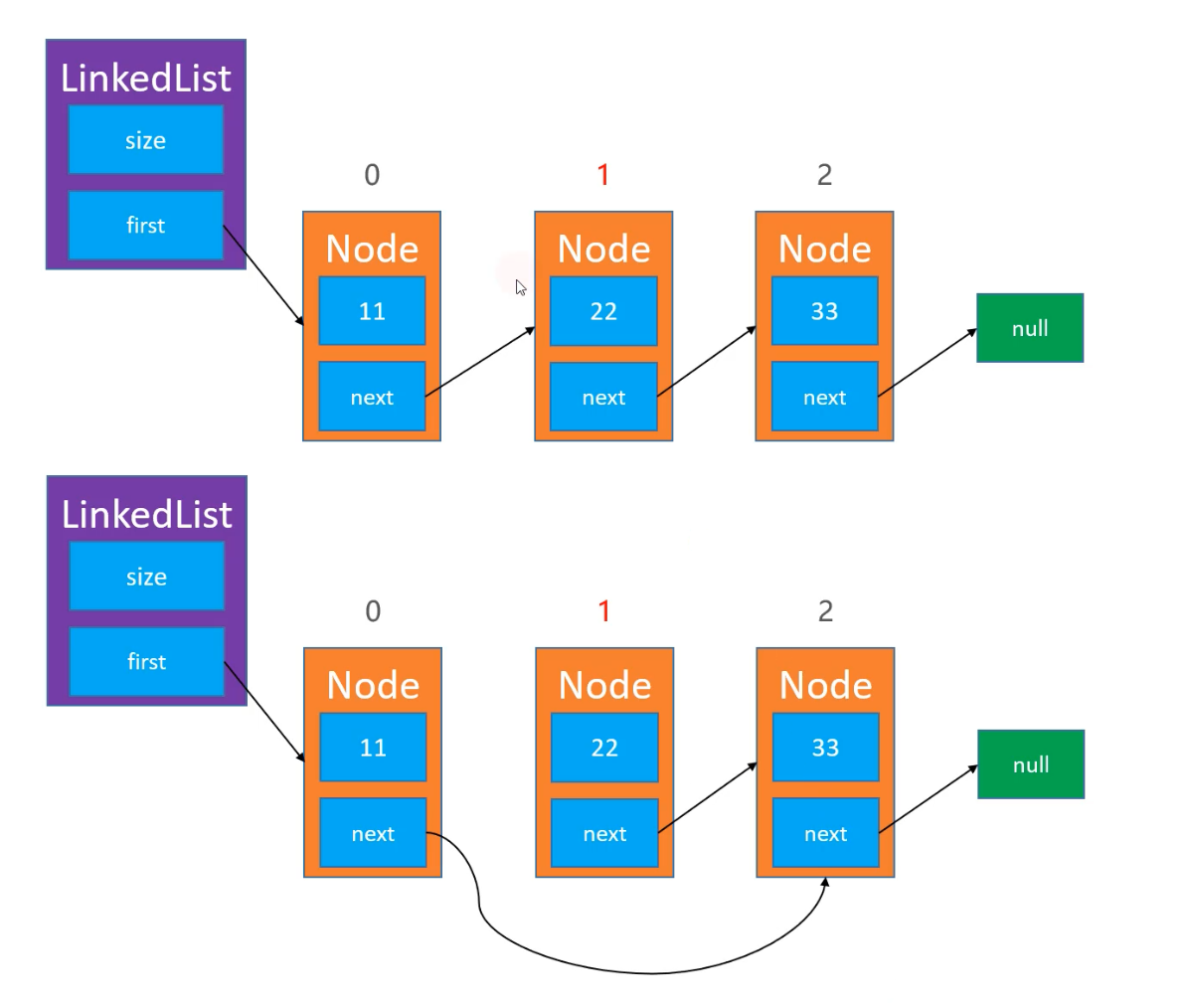
删除元素

删除元素同样需要拿到前一个位置的节点，只需要将此节点指向下一个的下一个节点即可；还是类似，需要考虑index = 0 这个特殊情况，当删除第一个节点时，只需要将 firstNode 指向它的 next ，之后就是 size-- 。

需要注意的是，这里删除以后需要返回被删除元素的值，首先可以定义一个节点用来存储被删的节点，可直接赋为 firstNode，如果不是删除头节点，可以再次赋值：

1
2
3
4
5
6
7
8
9
10
11
12
13
public E remove(int index) {
    rangeCheck(index);
    Node<E> node = firstNode;
    if (index == 0) {
        firstNode = node.next;
    } else {
        Node<E> prevNode = node(index - 1);
        node = prevNode.next;
        prevNode.next = prevNode.next.next;
    }
    size--;
    return node.element;
}

indexOf & toString

对于 indexOf 方法可以直接借鉴我们之前的动态数组 ArrayList，只需要做简单修改：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public int indexOf(E element) {
    Node<E> node = firstNode;
    if (element == null) {
        for (int i = 0; i < size; i++) {
            if (node.element == null) {
                return i;
            }
            node = node.next;
        }
    } else {
        for (int i = 0; i < size; i++) {
            if (element.equals(node(i).element)) {
                return i;
            }
            node = node.next;
        }
    }
    return ELEMENT_NOT_FOUND;
}

toString() 方法也是类似：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public String toString() {
    StringBuilder sBuilder = new StringBuilder();
    sBuilder.append("size:" + size).append(", [");
    Node<E> node = firstNode;
    for (int i = 0; i < size; i++) {
        if (i == 0) {
            sBuilder.append(node.element);
        } else {
            sBuilder.append(",").append(node.element);
        }
        node = node.next;
    }
    sBuilder.append("]");
    return sBuilder.toString();
}

虚拟头结点

因为在处理增删逻辑的时候，免不了对头结点进行一些特殊处理，有时候为了让代码更加精简，统一所有节点的处理逻辑，可以在最前面增加一个虚拟的不存储数据的头结点。

首先要增加一个构造函数，因为初始化的时候，虽没有元素，但也有一个虚拟的头结点：

1
2
3
4
// 这里复制了一份文件
public LinkedList_With_Fake_FirstNode() {
    firstNode = new Node<>(null, null);
}

其次是遍历链表的查找节点的 node() 方法和toString()需要调整，从虚拟头结点的 next 开始查找：

1
Node<E> node = firstNode.next;

之后是，添加和删除的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
@Override
public void add(int index, E element) {
    // 关键是这句判断的代码，之后即是统一的处理
    Node<E> prevNode = index == 0 ? firstNode : node(index - 1);
    Node<E> node = new Node<E>(element, prevNode.next);
    prevNode.next = node;
    size++;
}

@Override
public E remove(int index) {
    Node<E> prevNode = index == 0 ? firstNode : node(index - 1);
    Node<E> node = prevNode.next;
    prevNode.next = prevNode.next.next;
    size--;
    return node.element;
}

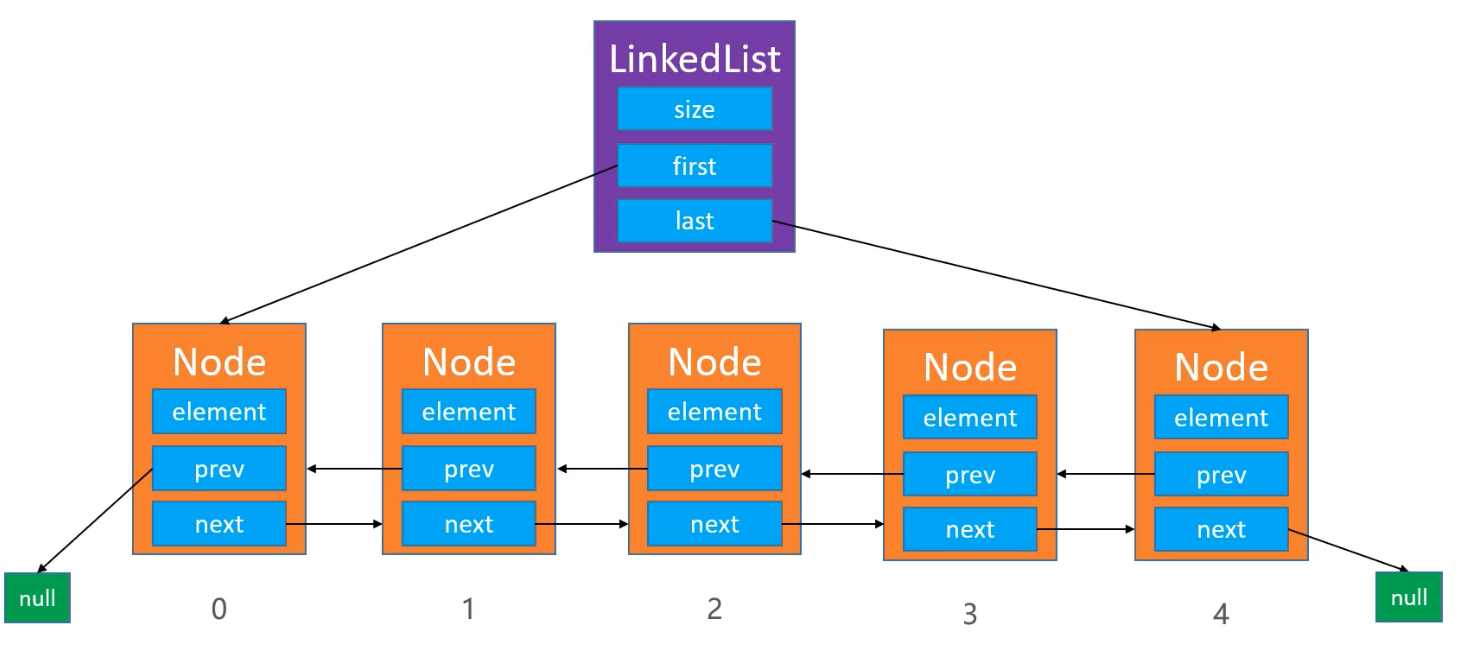
双向链表

上述学习的链表，也叫做单向链表，只能单向的寻找邻近的元素，双向链表顾名思义，使用双向链表可以提升链表的综合性能：

获取节点

当节点可以前后双向访问以后，首先要修改的应该是 node()方法，可以根据查找节点序列与动态数组长度的关系选择从前/后开始：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
private Node<E> node(int index) {
    rangeCheck(index);
    if (index < size >> 1) {
        Node<E> node = firstNode;
        for (int i = 0; i < index; i++) {
            node = node.next;
        }
        return node;
    } else {
        Node<E> node = lastNode;
        for (int i = size - 1; i > index; i--) {
            node = node.prev;
        }
        return node;
    }
}

清空元素

清空元素这个顺手就好了，这里涉及到清空元素方法调用后，元素节点是否还留存的问题，肯定是被回收的，这里涉及过多的 Java 虚拟机的知识，不多说了：

1
2
3
4
5
public void clear() {
    firstNode = null;
    lastNode = null;
    size = 0;
}

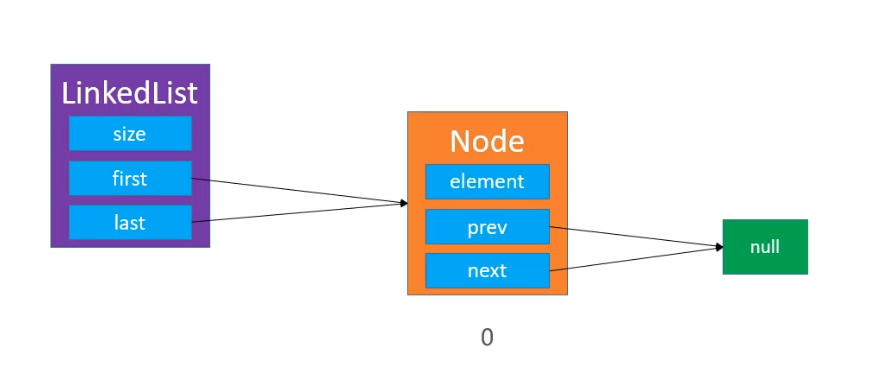
添加元素

需要注意的就是下图的特殊情况：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public void add(int index, E element) {
    rangeCheckForAdd(index);
    if (index == size) {	// 往尾部添加节点
        Node<E> node = new Node<E>(lastNode, element, null);
        if (lastNode == null) {	// 链表无节点时添加
            firstNode = node;
            lastNode = node;
        } else {
            lastNode.next = node;
            lastNode = node;
        }
    } else {
        Node<E> nextNode = node(index);
        Node<E> prevNode = nextNode.prev;
        Node<E> node = new Node<E>(prevNode, element, nextNode);
        if (prevNode == null) {
            firstNode = node;
        } else {
            prevNode.next = node;
        }
        nextNode.prev = node;
    }
    size++;
}

删除元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public E remove(int index) {
    rangeCheck(index);
    Node<E> deleteNode = node(index);
    Node<E> prevNode = deleteNode.prev;
    if (deleteNode.next == null) {	// 删除最后一个节点
        lastNode = prevNode;
    } else {
        deleteNode.next.prev = prevNode;
    }
    if (deleteNode.prev == null) {	// 删除第一个节点
        firstNode = deleteNode.next;
    } else {
        deleteNode.prev.next = deleteNode.next;
    }
    size--;
    return deleteNode.element;
}

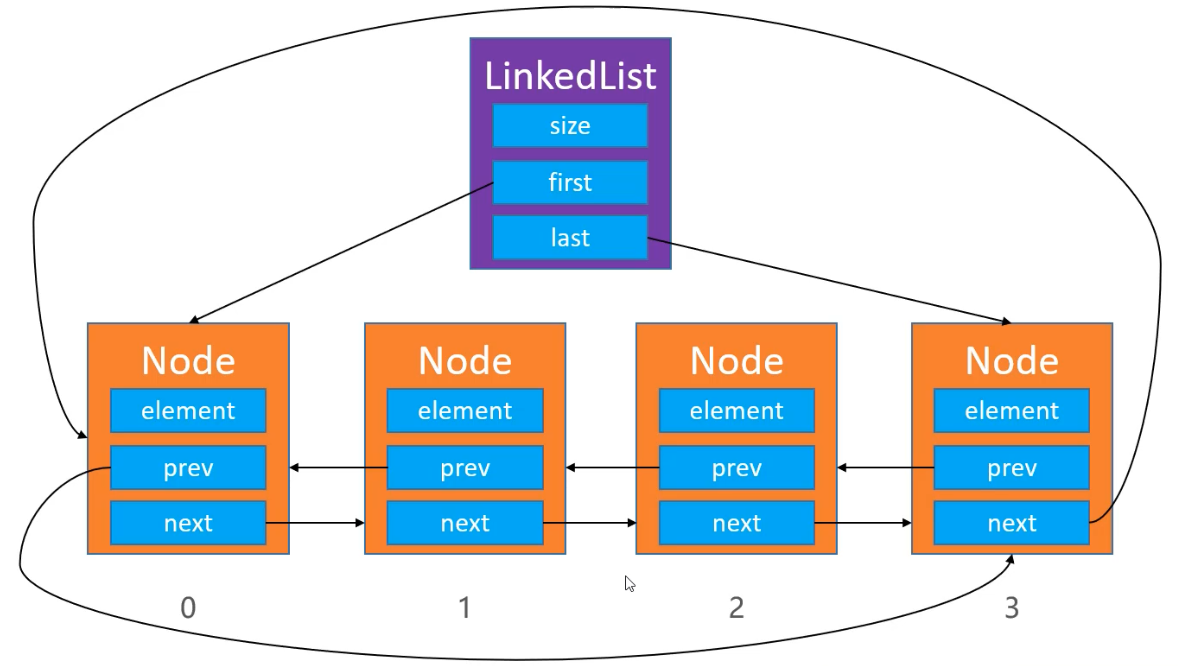
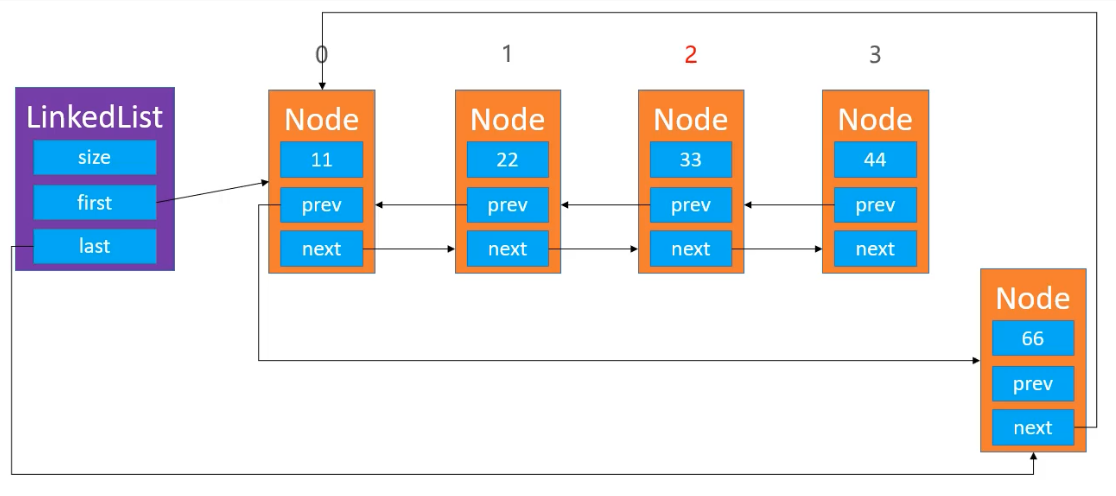
双向循环列表

image-20210425105646063

添加元素

需要考虑的也是这种特殊情况：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public void add(int index, E element) {
    rangeCheckForAdd(index);
    if (index == size) {
        Node<E> node = new Node<E>(lastNode, element, firstNode);
        if (lastNode == null) {
            firstNode = node;
            lastNode = node;
            node.next = node;
            node.prev = node;
        } else {
            lastNode.next = node;
            lastNode = node;
            firstNode.prev = node;
        }
    } else {
        Node<E> nextNode = node(index);
        Node<E> prevNode = nextNode.prev;
        Node<E> node = new Node<E>(prevNode, element, nextNode);
        if (prevNode == lastNode) {
            firstNode = node;
        } else {
            prevNode.next = node;
        }
        nextNode.prev = node;
    }
    size++;
}

删除元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public E remove(int index) {
    rangeCheck(index);
    Node<E> deleteNode = node(index);
    Node<E> prevNode = deleteNode.prev;

    deleteNode.next.prev = prevNode;
    prevNode.next = deleteNode.next;

    if (deleteNode == lastNode) { // index == size - 1
        lastNode = prevNode;
    }
    if (deleteNode == firstNode) { // index == 0
        firstNode = deleteNode.next;
    }
    size--;
    return deleteNode.element;
}

小练习-约瑟夫问题

我们先简单了解以下这个约瑟夫问题，摘自阿橋问题 - 维基百科，自由的百科全书 (wikipedia.org):

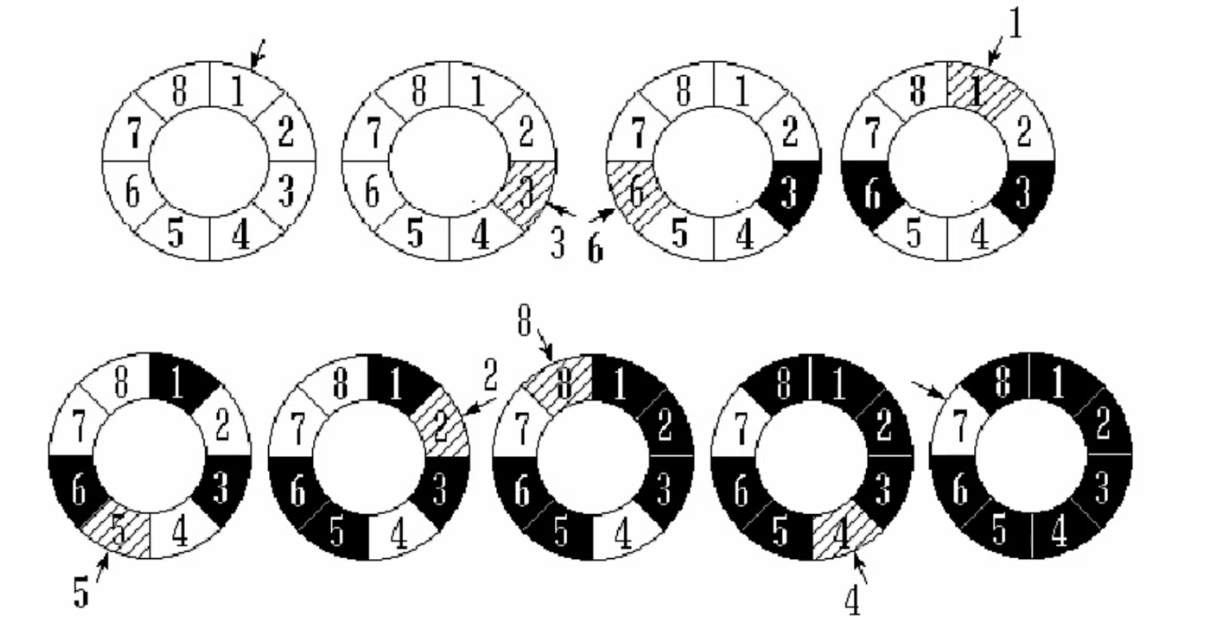
阿橋问题（有时也称为约瑟夫斯置换），是一个出现在计算机科学和数学中的问题。在计算机编程的算法中，类似问题又称为约瑟夫环。

人们站在一个等待被处决的圈子里。 计数从圆圈中的指定点开始，并沿指定方向围绕圆圈进行。 在跳过指定数量的人之后，处刑下一个人。 对剩下的人重复该过程，从下一个人开始，朝同一方向跳过相同数量的人，直到只剩下一个人，并被释放。

问题即，给定人数、起点、方向和要跳过的数字，选择初始圆圈中的位置以避免被处决。

这个问题比较简单的做法是用循环单链表模拟整个过程，正好我们刚把链表梳理了一遍，为了更好地解决此问题，我们可以考虑增加 1 个成员变量，3 个方法：

  • current：用于指向某个节点；
  • void reset();：让 current 指向头结点 first ；
  • E next();：让 current 移动一步，也就是 current = current.next;；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
private Node<E> current;

public void reset() {
    current = firstNode;
}

public E next() {
    if (current == null) {
        return null;
    } else {
        current = current.next;
        return current.element;
    }
}

具体的思路是，首先将 current 指向头结点，之后每次移动指定的次数，然后删除元素，删除元素后，要判断是否是最后一个元素，需要让current 移动一位，将删除的元素的位置腾出来，且删除元素时是删除current 这个元素，所以需要修改以下，可直接再增加一个removeNode()方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public E removeNode() {
    if (current == null) {
        return null;
    } else {
        Node<E> deleteNode = current;
        System.out.println(current.element);
        Node<E> prevNode = deleteNode.prev;

        deleteNode.next.prev = prevNode;
        prevNode.next = deleteNode.next;

        if (deleteNode == lastNode) { // index == size - 1
            lastNode = prevNode;
        }
        if (deleteNode == firstNode) { // index == 0
            firstNode = deleteNode.next;
        }
        size--;
        // 下一个元素为 null 说明是最后一个元素
        if (current.next != null) {
            current = current.next;
        }
        return deleteNode.element;
    }
}

我们再编写一个静态方法来测试：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
static void josephusTest(CircleLinkedList_josephus<Integer> list, int num, int pace) {
    for (int i = 0; i < num; i++) {
        list.add(i + 1);
    }
    list.reset();
    System.out.println(list);

    while (!list.isEmpty()) {
        for (int i = 0; i < pace; i++) {
            list.next();
        }
        list.removeNode();
    }
}

public static void main(String[] args) {
    CircleLinkedList_josephus<Integer> josephus = new CircleLinkedList_josephus<>();
    josephusTest(josephus, 8, 2);
}

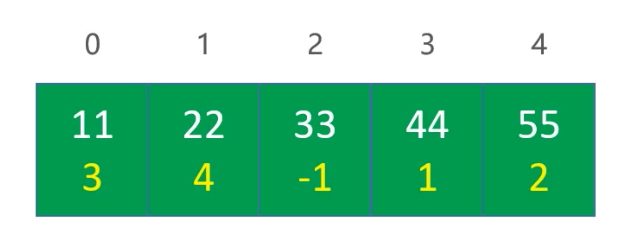
静态链表

前面所学习的链表，是依赖于指针（引用）实现的， 有些编程语言是没有指针的，比如早期的 BASIC、FORTRAN 语言，没有指针的情况下，如何实现链表？
可以通过数组来模拟链表，称为静态链表。数组的每个元素存放 2 个数据：值、下个元素的索引，数组 0 位置存放的是头结点信息。

Prev
2019-10-16 21:27:24 #数据结构与算法
Next