数据结构与算法学习之AVL树

2022-06-27 14:46:50 #数据结构与算法

基本概念

AVL 是最早发明的自平衡二叉搜索树之一，名称来源于 G. M. Adelson-Velsky 和 E. M. Landis (两位来自苏联的科学家)；

平衡因子：某节点的左右子树的高度差；

而在 AVL 树中每个节点的平衡因子只能是 1，0，-1；

即绝对值 ≤ 1，大于 1 则称之为失衡；也就是说每个节点的左右子树高度差不超过 1；搜索、添加、删除的时间复杂度是 O(logn)；

添加的失衡

当在二叉搜索树中添加一个元素时，最坏的情况可能会导致所有祖先都失衡，父节点其他的非祖先节点不会失衡；

添加导致的失衡可以通过旋转节点进行调整高度，达到重新平衡，有四种情况：

LL - 右旋转

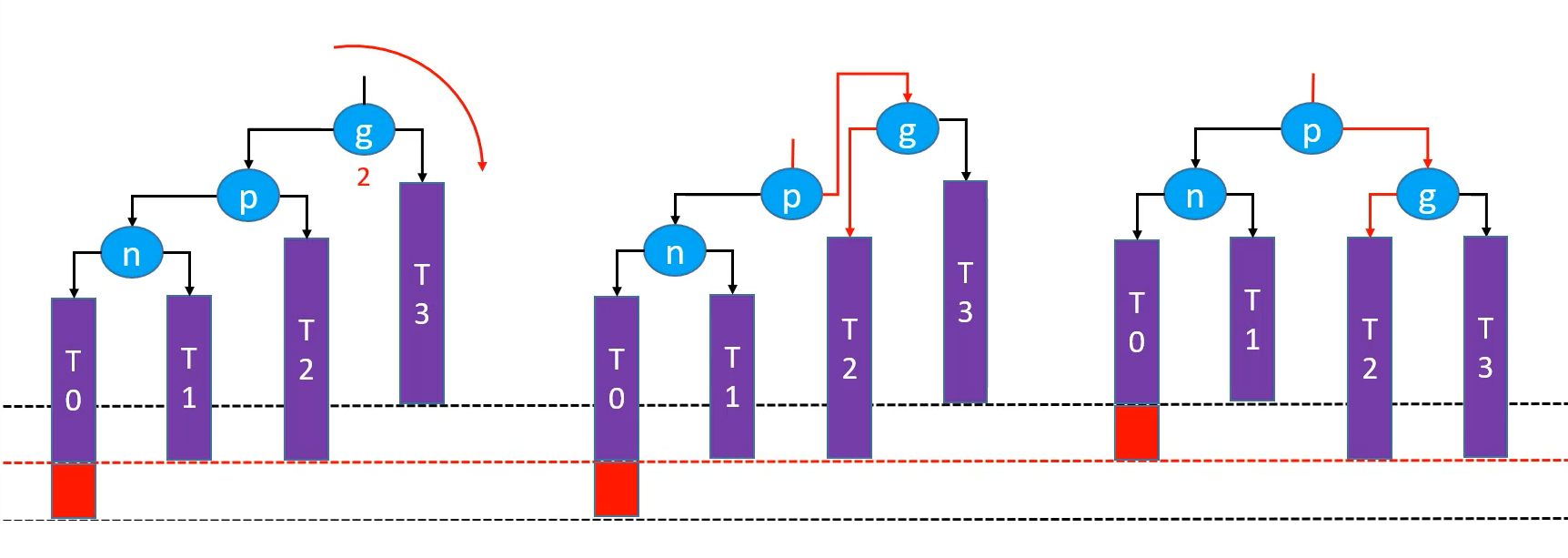
首先解释一下这个分类名称，LL 表示新添加的节点 n 是在由其导致失衡的最近的祖先节点即 g 节点的 left 的 left 处；而有右旋转是将这种失衡状态重新平衡的方法，即：

g.left = p.right
p.right = g
让 p 成为该子树的根节点
维护 parent 以及更新节点高度

经过旋转之后，仍然是一颗二叉搜索树：T0 < n < T1 < p < T2 < g < T3；

RR - 左旋转

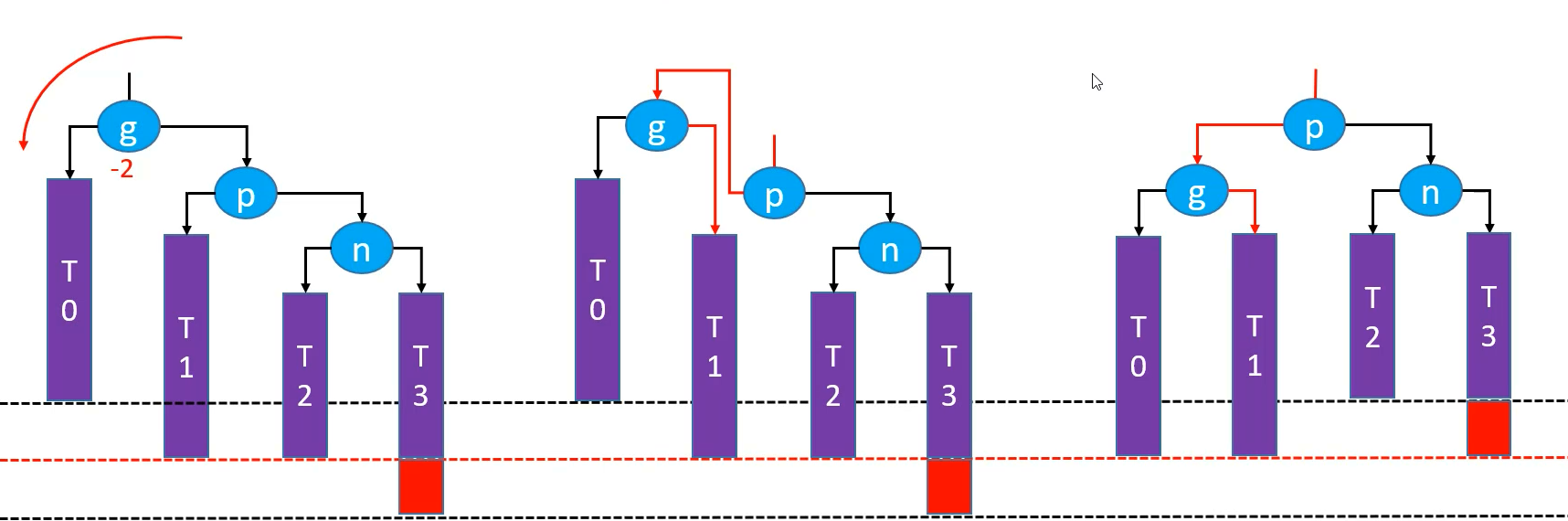
g.right= p.left
p.left= g
让 p 成为该子树的根节点；
维护 parent 以及更新节点高度；

LR - 左旋转，右旋转

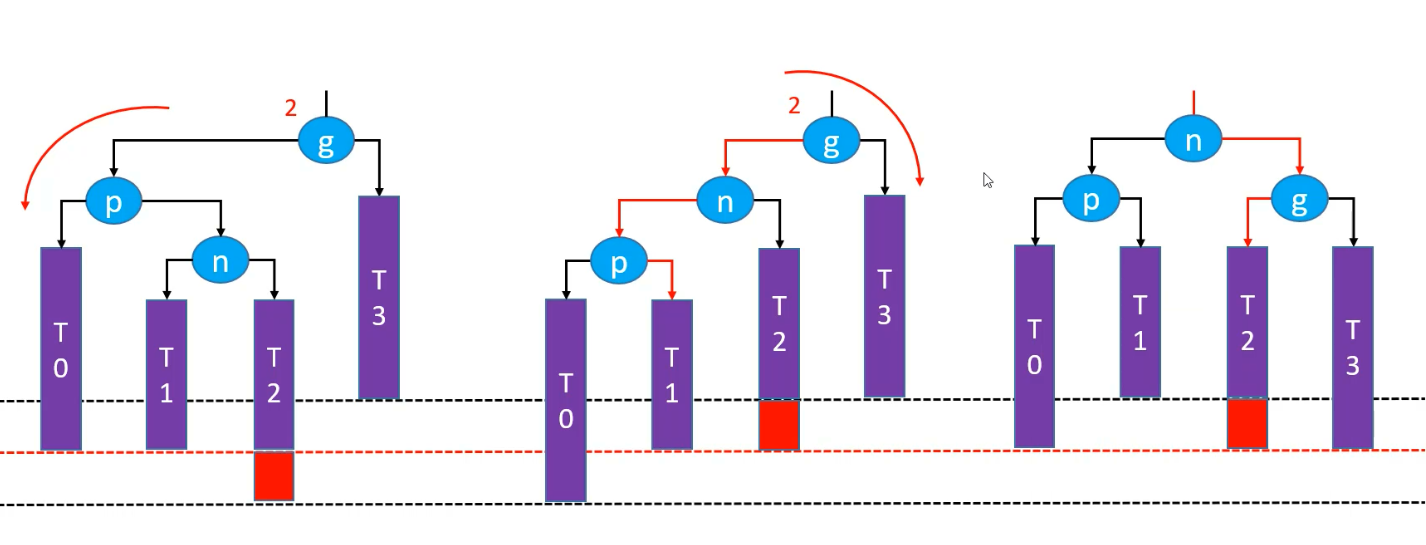
经过两次旋转：先将 p 节点左旋，即形成 LL 情况，再右旋 g 节点；

RL - 右旋转，左旋转

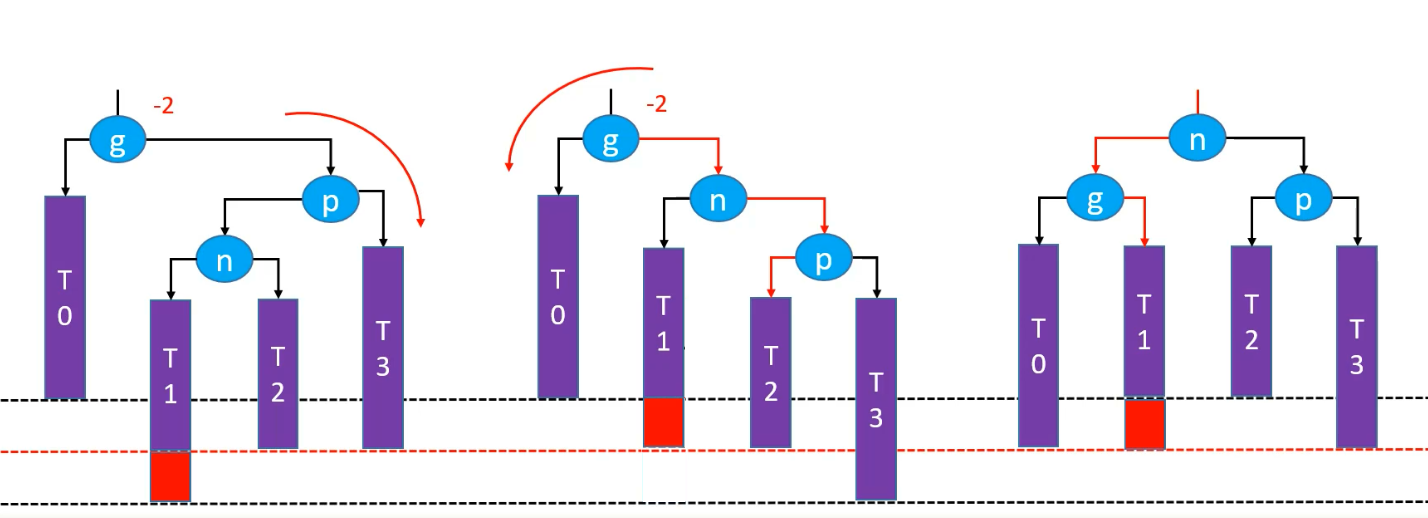
经过两次旋转：先将 p 节点右旋，即形成 RR 情况，再左旋 g 节点；

失衡调整

我们在BinarySearchTree内部添加一个空方法afterAdd，每次添加后调用该方法：

public void add(E element) {
    if(root == null) {
        size++;
        afterAdd(root);
        return;
    }
    //...
    size++;
    afterAdd(newNode);
}

然后让AVL继承BinarySearchTree，重写afterAdd方法，即可完成失衡调整逻辑；

失衡调整逻辑如下：

沿着添加的节点的parent属性，往上找；
找到最近的失衡节点，进行旋转调整；

那么如何判断一个节点是否失衡呢，当然是检测其平衡因子了，即需要一个方法返回检测结果：

private static class AVLNode<E> extends Node<E> {
    int height = 1;
    public AVLNode(E element, Node<E> parent) {
        super(element, parent);
    }
    public int balanceFactor() {
        int leftHeight = left == null ? 0 : ((AVLNode<E>)left).height;
        int rightHeight = right == null ? 0 : ((AVLNode<E>)right).height;
        return leftHeight - rightHeight;
    }
}

private boolean isBanlance(Node<E> node) {
    return Math.abs(((AVLNode<E>)node).balanceFactor()) <= 1; 
}

因此，在 AVL 树中也定义了一个 AVL 节点类继承自二叉树的节点类，还需要修改搜索二叉树中创建逻辑（创建的是默认的节点）：

// BinaryTree.java
protected Node<E> createNode(E element, Node<E> parent){
    return new Node<E>(element, parent); 
}
// BinarySearchTree.java
public void add(E element) {
    // root = new Node<E>(element, null); 
    root = createNode(element, null); 
}
// AVLTree.java
@Override
protected Node<E> createNode(E element, Node<E> parent) {
    return new AVLNode<>(element, parent);
}

更新高度

每次添加的新节点，高度是 1，即在AVLNode中的初始值为 1；之后沿着parent属性往上遍历，主要情况有三种：

祖先节点的高度平衡的，那么更新高度；
祖先节点的高度不平衡，即调整失衡；
遍历到祖先节点为 null，停止；

由此，需要编写一个更新高度的私有方法：

private void updateHeight(Node<E> node){
    ((AVLNode<E>)node).updateHeight();
}
private static class AVLNode<E> extends Node<E> {
	public void updateHeight() {
		int leftHeight = left == null ? 0 : ((AVLNode<E>)left).height;
		int rightHeight = right == null ? 0 : ((AVLNode<E>)right).height;
		height = 1 + Math.max(leftHeight, rightHeight);
	}
}

恢复平衡

当往上遍历时，检测到失衡节点，即需要进行调整，那么就需要对几种类型（RR，LL等）进行判断，那么还需要几个简单的方法：

// BinaryTree.java
protected static class Node<E>{
    public boolean isLeftChild() {
        return parent != null && this == parent.left;
    }
    public boolean isRightChild() {
        return parent != null && this == parent.right;
    }
}

为了调整失衡节点 g ，我们还需要获取到构成结构的 p 节点和 n 节点，通过上述的结构图，不难观察到 p 是 g 的高度较大的子节点，同样 n 也如出一辙，即还需要一个获取高度更高的子节点的方法：

private static class AVLNode<E> extends Node<E> {
    public Node<E> tallerChild(){
        int leftHeight = left == null ? 0 : ((AVLNode<E>)left).height;
        int rightHeight = right == null ? 0 : ((AVLNode<E>)right).height;
        if(leftHeight > rightHeight) return left;
        if(rightHeight > leftHeight) return right;
        return isLeftChild() ? left : right;
    }
}

那么恢复平衡的方法也就很自然的写出来了：

@Override
protected void afterAdd(Node<E> node) {
    while((node = node.parent) != null) {
        if(isBanlance(node)) {
            updateHeight(node); // 更新高度
        }else {
            rebalance(node); // 恢复平衡
            break;
        }
    }
}

旋转方向判断

有了上述的基本判断方法和逻辑框架，那么就可以编写失衡调整的方法了，其中主要涉及的是结构的旋转方向的判断，根据节点之间的连线，也就是isLeftChild或isRightChild方法即可：

private void rebalance(Node<E> grand) {
    Node<E> parent = ((AVLNode<E>)grand).tallerChild();
    Node<E> node = ((AVLNode<E>)parent).tallerChild();
    if(parent.isLeftChild()) { // L
        if(node.isLeftChild()) { // LL
            rotateRight(grand);
        }else { // LR
            rotateLeft(parent);
            rotateRight(grand);
        }
    }else {	// R
        if(node.isLeftChild()) { // RL
            rotateRight(parent);
            rotateLeft(grand);
        }else { //RR
            rotateLeft(grand);
        }
    }
}

左旋实现

private void rotateLeft(Node<E> grand){
    Node<E> parent = grand.right;
    Node<E> child = parent.left;
    // 旋转
    grand.right = child;
    parent.left = grand;
    afterRotate(grand, parent, child);
}

右旋实现

private void rotateRight(Node<E> grand){
    Node<E> parent = grand.left;
    Node<E> child = parent.right;
    // 旋转
    grand.left = child;
    parent.right = grand;
    afterRotate(grand, parent, child);
}

因为无论是左旋还是右旋，后序的维护 parent 和更新高度的代码都是一样的，所以抽离到了一个函数中：

private void afterRotate(Node<E> grand,Node<E> parent,Node<E> child) {
    // 维护 parent --> grand.parent, parent 成为子树根节点 
    parent.parent = grand.parent;
    if(grand.isLeftChild()) {
        grand.parent.left = parent;
    }else if(grand.isRightChild()){
        grand.parent.right = parent;
    }else {
        root = parent;
    }
    // 维护 grand --> parent
    grand.parent = parent;

    // 维护 child --> grand
    if(child != null) {
        child.parent = grand;
    }
    // 更新高度
    updateHeight(grand);
    updateHeight(parent);
}

统一旋转操作

删除的失衡

只可能会导致父节点或祖先节点失衡，其他节点都不可能失衡；
删除节点进行一次失衡调整后，更高层的祖先节点也可能失衡，需要再次调整，往复……

那么只需要将添加失衡调整代码中的一次调整后的break语句删除即可，其他的操作一致：

@Override
protected void afterRemove(Node<E> node) {
    while((node = node.parent) != null) {
        if(isBanlance(node)) {
            updateHeight(node); // 更新高度
        }else {
            rebalance(node); // 恢复平衡
        }
    }
}

总结

添加节点

可能会导致所有祖先节点都失衡
只要让高度最低的失衡节点恢复平衡，整棵树就恢复平衡【仅需O(1)次调整】

删除节点

只可能会导致父节点或祖先节点失衡，让父节点恢复平衡后，可能会导致更高层的祖先节点失衡【最多需要O(logn)次调整】

平均时间复杂度

搜索：O(logn)
添加：O(logn)，仅需O(1)次的旋转操作
删除：O(logn)，最多需要 O(logn)次的旋转操作

2022-06-27 14:46:50 #数据结构与算法