数据结构与算法学习之复杂度
2019-10-15 21:34:24 #数据结构与算法

什么是算法

算法就是用于解决特定问题的一系列的执行步骤，例如：

1
2
3
4
5
6
7
8
9
10
11
12
// 计算 a + b 的值
public static int plus(int a,int b) {
    return a + b;
}
// 计算 1 ~ n 和的值
public static int sum(int n) {
    int result = 0;
    for (int i = 0;i<=n;i++) {
        result += i;
    }
    return result;
}

使用不同的算法，解决同一个问题，效率可能相差非常大，比如求解第 n 个斐波那契数（Fibonacci number），这里先埋一个伏笔，具体我们后面再说。

如何评判一个算法的好坏

如果单从执行的效率上进行评估，可能会想到这么一种方案，比较不同算法对同一组输入的处理执行时间，当然这样的方案也叫做：事后统计法。

这样的方案有比较明显的缺点，执行的时间严重依赖运行时各种不确定的环境因素，必须编写相应的测算代码，而且测试的数据的选择也比较难以保证公平性。

一般从以下几个维度来评估算法的优劣：

  • 正确性，可读性，健壮性（对不合理输入的反应能力和处理能力）；

  • 时间复杂度（time complexity）：估算赋值语句的执行次数（执行时间）；

    一条赋值语句同时包含了（表达式）计算和（变量） 存储两个基本资源。

  • 空间复杂度（space complexity）：估算所需占用的存储空间；

大O表示法

一般用大O表示法来描述复杂度，它表示的是数据规模 n 所对应的复杂度，在描述时会忽略常数，和n 的系数，以及 n 的低阶，例如：

  • 9 >> O(1)
  • 2n + 3 >> O(n)
  • n2 + 2n + 6 >> O(n2)
  • 4n3 + 3n2 + 22n + 100 >> O(n3)

需要注意，大O表示法仅仅只是一种粗略的分析模型，是一种估算，能帮助我们短时间内了解一个算法的执行效率。

对数阶的细节

对于对数阶，一般会忽略底数，因为
$$
log_{2}{n} = log_{2}{9} \times log_{9}{n}
$$
所以 $log_{2}{n}$，$log_{2}{9}$ 统称 $log{n}$ 。

小练习

无论传入的 n 的值为多大，下列代码都只执行 1 + 1 + 4 + 4 + 4 = 14 个运算步骤（暂且忽略判断语句），所以时间复杂度为 O(1)，其余的以此类推。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public static void test1(int n) {
    // 1
    if (n > 10) { 
        System.out.println("n > 10");
    } else if (n > 5) { 
        System.out.println("n > 5");
    } else {
        System.out.println("n <= 5"); 
    }

    // 1 + 4 + 4 + 4
    for (int i = 0; i < 4; i++) {
        System.out.println("test");
    }
    // O(1)
}

public static void test2(int n) {
    // 1 + 3n  >>  O(n)
    for (int i = 0; i < n; i++) {
        System.out.println("test");
    }
}

public static void test3(int n) {
    // 1 + 2n + n * (1 + 3n)
    // 3n^2 + 3n + 1  >>  O(n^2)
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            System.out.println("test");
        }
    }
}

以下代码，while 循环在 (n = n / 2) > 0 不满足时停止循环，也就是看 n 能被 2 整除几次，联系到数学的运算就是 log，这样说不能很好的理解，举个例子，当传入 n = 8 时，8/2 = 4，4/2 = 2，2/2 = 1，1/2 = 0，到第四次就不满足停止循环，也就是循环 3 次，即 8 = 23 >> 3 = log2(8)；同理，test6 中 n/5 和 test7 中 i = i * 2，也是类似的处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public static void test5(int n) {
    // 执行次数 = log2(n)  >>  O(logn)
    while ((n = n / 2) > 0) {
        System.out.println("test");
    }
}

public static void test6(int n) {
    // log5(n)  >>  O(logn)
    while ((n = n / 5) > 0) {
        System.out.println("test");
    }
}

public static void test7(int n) {
    // 1 + 2*log2(n) + log2(n) * (1 + 3n)
    // 1 + 3*log2(n) + 2 * nlog2(n)  >>  O(nlogn)
    for (int i = 1; i < n; i = i * 2) {
        // 1 + 3n
        for (int j = 0; j < n; j++) {
            System.out.println("test");
        }
    }
}

常见的复杂度

执行次数 复杂度 非正式用语
12 O(1) 常数阶
2n + 3 O(n) 线性阶
4n2 + 2n + 6 O(n2) 平方阶
4log2n +25 O(logn) 对数阶
3n + 2nlog3n + 15 O(nlogn) nlogn 阶
4n3 + 3n2 +22n + 100 O(n3) 立方阶
2n O(2n) 指数阶

复杂度大小：O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)

可以把复杂度当作函数，利用工具形象对比复杂度的大小：

数据规模较小时

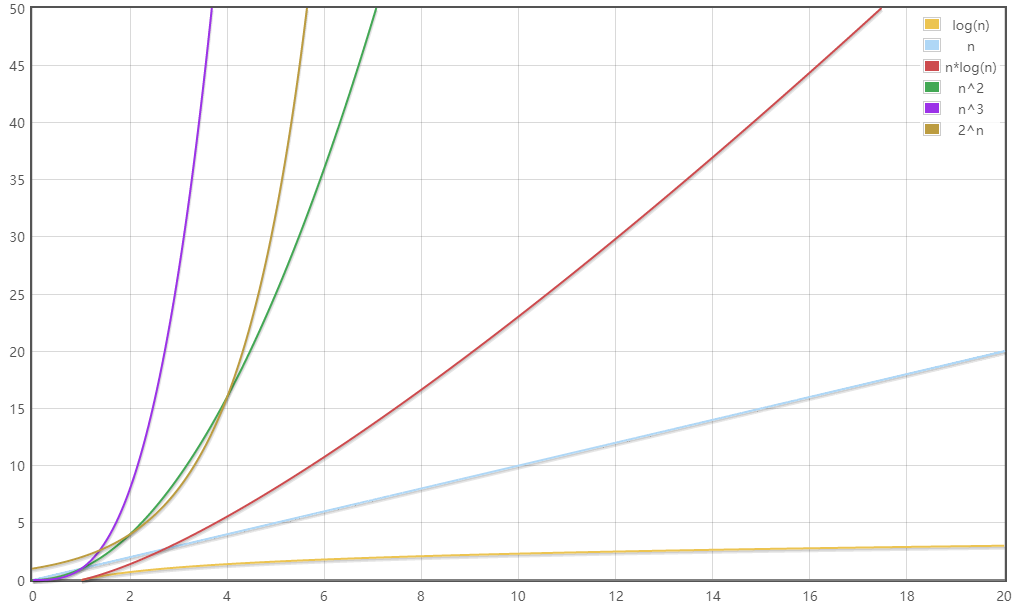
数据规模较大时

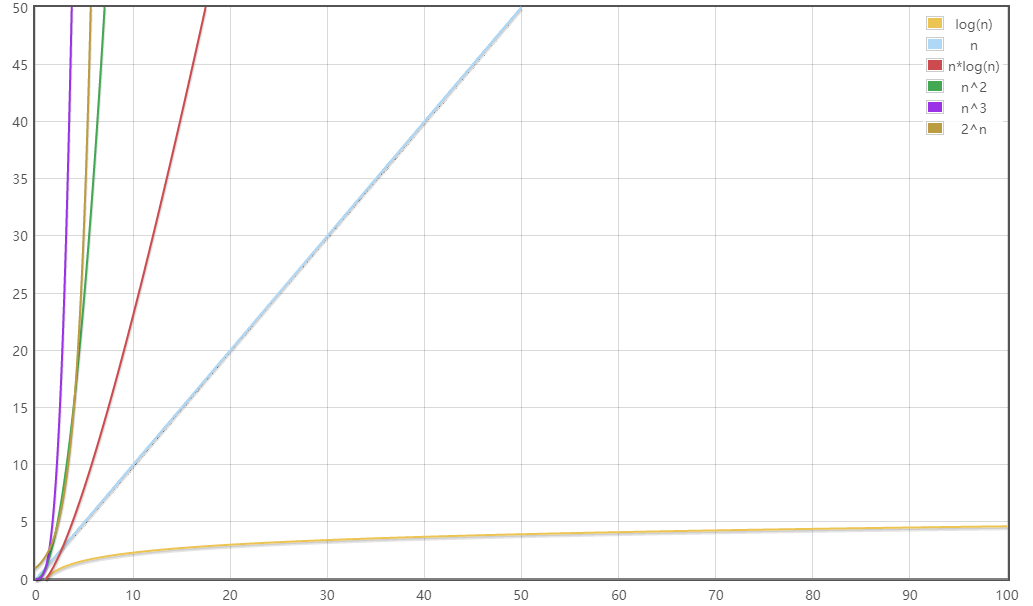
斐波那契函数算法分析

对于斐波那契函数，即返回斐波那契数列的第 n 位这样的一个函数的写法一般有两种：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static int fib1(int n) {
    if (n <= 1)
        return n;
    return fib1(n - 1) + fib1(n - 2);
}

public static int fib2(int n) {
    if (n <= 1)
        return n;
    int first = 0;
    int second = 1;
    for (int i = 0; i < n - 1; i++) {
        second += first;
        first = second - first;
    }
    return second;
}

仅从代码量来看，是 fib1 完胜，但我们抛开表面深挖底层可以发现事情远不止这么简单，我们可以先用代码分别测算它们的执行时间来看个大概：

【fib1(10)】耗时：0.0秒 【fib2(10)】耗时：0.0秒

【fib1(45)】耗时：10.374秒 【fib2(45)】耗时：0.0秒

当数据规模较小时，时间差并不是很大，数据规模大到一定程度，两者之间的区别就出来了，我们可用大O表示法来粗略确定他们的时间复杂度，就明白这么回事了。

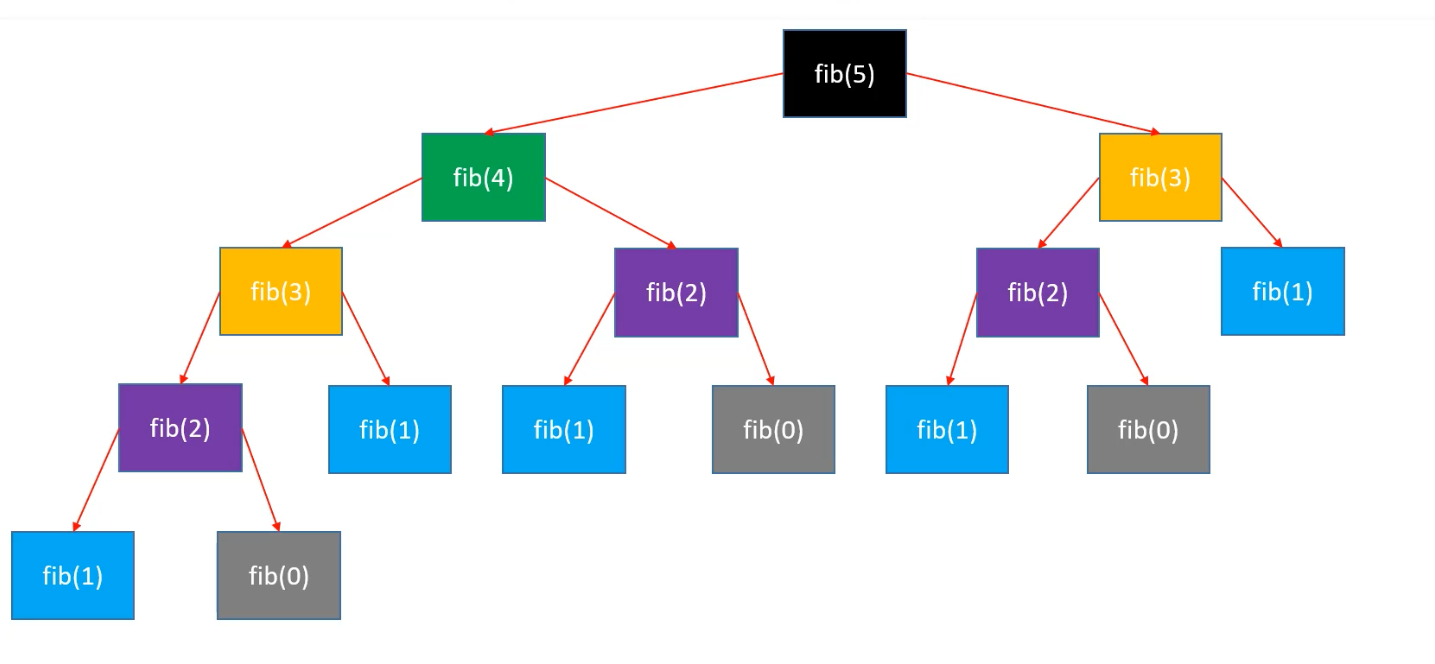
因为 fib1() 函数内的 return 语句可看作函数的核心，即时间复杂度可由调用该函数的次数来确定。

由图可知，1 + 2 + 4 + 8 = 2^0^ + 2^1^ + 22 + 23 = 2^4^− 1 = 2^n−1^− 1 = 0.5 ∗ 2n− 1，所以时间复杂度是 O(2n)。

而 fib2() 的时间复杂度很容易确定为 O(n)，它们的区别有多大呢？

如果有一台1GHz的普通计算机，运算速度109次/秒（n为64），O(n)大约耗时6.4 ∗ 10-8秒，O(2n)大约耗时584.94年。有时候算法之间的差距，往往比硬件方面的差距还要大。

Prev
2019-10-15 21:34:24 #数据结构与算法
Next